Hue Luminance and Saturation (HLS) Model and Manipulating Colours

Pick and manipulate colours more easily

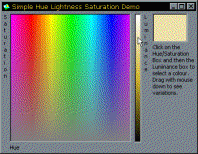
Normally in computers colours are described in terms of their Red, Green and Blue components. Whilst you can specify all displayable colours this way, it leaves something to be desired when it comes to picking a colour. For example, most people find it very difficult to determine what RGB values you would use to create a Pink or Brown colour (try it!). The HLS model provides a more intuitive method and enables you to create lighter/darker or more intense/less intense versions of colours very easily.

The Hue, Luminance and Saturation Model

There are numerous colour models which attempt to work around the limitations of RGB and provide a more intuitive way of getting to the colour you want. One of the easiest, and most frequently used, is the Hue, Luminance and Saturation (HLS) Model.

This HLS model describes colours in the following terms:

• Hue
  The horizontal axis of the box in the demonstration project picture, which varies from magenta - red - yellow - green - cyan - blue - magenta.
• Saturation
  The vertical axis of the box, and describes how intense (saturated) or "grey" (unsaturated) the colour is.
• Luminance
  The second picture box in the demonstration project picture, which and varies from black (0 luminace) through to the brightest version of the colour itself.

With this model it is easier to pick a colour and it allows you to do things in code which you can't really achieve with RGB. Examples are determining what a lighter or darker tone of a given RGB colour is (by modifying the Luminance), creating a more washed out colour (by modifying the Saturation) or colourising a whole image (by modifying the Hue).

Coding the HLS Model

Normally Hue is expressed as an angle between 0-360 to describe the colour and a value between 0 and 1 (a percentage) to describe Hue and Saturation. I have missed out the conversion to an angle in this implementation so the Hue works as follows:

Hue   Colour 
 -1   Magenta 
  0   Red 
  1   Yellow 
  2   Green 
  3   Aqua 
  4   Blue 
  5   Magenta 

Here is the code to do a conversion between HLS and RGB and vice-versa:

Public Sub RGBToHLS( _ 
    ByVal r As Long, ByVal g As Long, ByVal b As Long, _ 
    h As Single, s As Single, l As Single _ 
    ) 
Dim Max As Single 
Dim Min As Single 
Dim delta As Single 
Dim rR As Single, rG As Single, rB As Single 

    rR = r / 255: rG = g / 255: rB = b / 255 

    '{Given: rgb each in [0,1]. 
    ' Desired: h in [0,360] and s in [0,1], except if s=0, then h=UNDEFINED.} 
    Max = Maximum(rR, rG, rB) 
    Min = Minimum(rR, rG, rB) 
    l = (Max + Min) / 2'{This is the lightness} 
        
    '{Next calculate saturation} 
    If Max = Min Then 
        'begin {Acrhomatic case} 
        s = 0 
        h = 0 
        'end {Acrhomatic case} 
    Else 
        'begin {Chromatic case} 
        '{First calculate the saturation.} 
        If l <= 0.5 Then 
            s = (Max - Min) / (Max + Min) 
        Else 
            s = (Max - Min) / (2 - Max - Min) 
        End If 
        '{Next calculate the hue.} 
        delta = Max - Min 
        If rR = Max Then 
            '{Resulting color is between yellow and magenta} 
            h = (rG - rB) / delta
        ElseIf rG = Max Then 
            '{Resulting color is between cyan and yellow}  
            h = 2 + (rB - rR) / delta 
        ElseIf rB = Max Then 
            '{Resulting color is between magenta and cyan} 
            h = 4 + (rR - rG) / delta 
        End If 
        'end {Chromatic Case} 
    End If 
End Sub 

Public Sub HLSToRGB( _ 
    ByVal h As Single, ByVal s As Single, ByVal l As Single, _ 
    r As Long, g As Long, b As Long _ 
    ) 
Dim rR As Single, rG As Single, rB As Single 
Dim Min As Single, Max As Single 

    If s = 0 Then 
        ' Achromatic case: 
        rR = l: rG = l: rB = l 
    Else 
        ' Chromatic case: 
        ' delta = Max-Min 
        If l <= 0.5 Then 
            's = (Max - Min) / (Max + Min) 
            ' Get Min value: 
            Min = l * (1 - s) 
        Else 
            's = (Max - Min) / (2 - Max - Min) 
            ' Get Min value: 
            Min = l - s * (1 - l) 
        End If 
        ' Get the Max value: 
        Max = 2 * l - Min 
    
        ' Now depending on sector we can evaluate the h,l,s: 
        If (h < 1) Then 
            rR = Max 
            If (h < 0) Then 
                rG = Min 
                rB = rG - h * (Max - Min) 
            Else 
                rB = Min 
                rG = h * (Max - Min) + rB 
            End If 
        ElseIf (h < 3) Then 
            rG = Max 
            If (h < 2) Then 
                rB = Min 
                rR = rB - (h - 2) * (Max - Min) 
            Else 
                rR = Min 
                rB = (h - 2) * (Max - Min) + rR 
            End If 
        Else 
            rB = Max 
            If (h < 4) Then 
                rR = Min 
                rG = rR - (h - 4) * (Max - Min) 
            Else 
                rG = Min 
                rR = (h - 4) * (Max - Min) + rG 
            End If         
        End If             
    End If 
    r = rR * 255: g = rG * 255: b = rB * 255 
End Sub 

Private Function Maximum(rR As Single, rG As Single, rB As Single) As Single 
    If (rR > rG) Then 
        If (rR > rB) Then 
            Maximum = rR 
        Else 
            Maximum = rB 
        End If 
    Else 
        If (rB > rG) Then 
            Maximum = rB 
        Else 
            Maximum = rG 
        End If 
    End If 
End Function 

Private Function Minimum(rR As Single, rG As Single, rB As Single) As Single 
    If (rR < rG) Then 
        If (rR < rB) Then 
            Minimum = rR 
        Else 
            Minimum = rB 
        End If 
    Else 
        If (rB < rG) Then 
            Minimum = rB 
        Else 
            Minimum = rG 
        End If 
    End If 
End Function 

Limitations of the HLS Model

Whilst the HLS Model is simple to implement, and gives a relatively easy colour picking interface, it is not a physically accurate model. That is to say, linear changes in luminance, hue or saturation do not correspond to a linear change in colour to the eye. More accurate models which overcome these limitations exist, such as the CIE scheme, but I've yet to understand these enough to work them out! Anyway, HLS works well enough unless you are interested in exact colour matching and processing between different display devices.